Peter H. van der Kamp

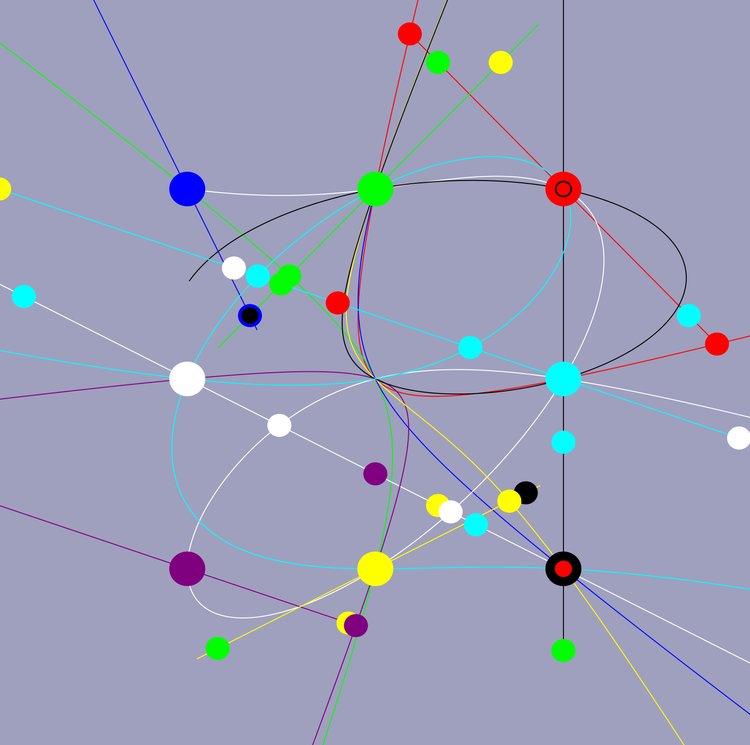
Transitioning

The curves in Passing through a crunode and On the cusp are quartic curves which all visit the same two points twice, i.e. they come from the same pencil (family) of infinitely many curves with two singular base points.

Each curve in this pencil has its own identity. They can have more singular points than another and the nature of such points may differ.

In Transitioning curves and colours change their appearance. It is ongoing. However, certain crucial changes happen over a short period of time.

Eight implies nine

Eight implies nine is a statement about cubic curves known as the Cayley–Bacharach theorem. A cubic curve which goes through eight given points also goes through a ninth point which depends only on the eight points given.

It follows that whenever two (or more) cubic curves meet in eight points, then they also meet in a ninth point.

Study of the ninth

Study of the ninth investigates what happens to the ninth point, cf. Eight implies nine, if one of eight points (arranged on a square) moves over a straight line.

Each straight line has the same colour as the point which moves on it. The straight line ends when the ninth gets out of sight. The straight line continues (out of sight) when the ninth is still visible. Whenever the induced curve on which the ninth travels passes one of the other eight points, a point with the same colour is placed on the straight line.

It is remarkable that the ninth point visits many (but not all) of the seven points. The constellation is as intriguing as the motion of celestial bodies in the sky due to gravitational interaction. Here, however, the cause is purely geometrical.

Going around in circles

Going around in circles is another Study of the ninth. It investigates what happens to the ninth point if one of the eight points (arranged on a grid) moves around in a circle.

Surprising observations were made. If the circle was sufficiently big the ninth point would visit all seven other points. However, the circles in Going around in circles were chosen small enough so that only a few of the other points are met.

Looks are deceiving. By complexifying the small circles one can find (determine) points on it such that the ninth point does indeed visit all seven other points.

Imagine all circles, big and small, attached to eight points. And imagine being the ninth, travelling in loops passing through the same points over and over again, a face, scowled in frustration.

Consideration

Consideration is dedicated to my father, whose approach to life, and art, is quite considerate.

The concentric circles are level-sets of a quadratic polynomial. Like in enthusiasm, three curves are tangent to a parabola. In Consideration only those special curves were chosen. One of them is combined (colour-wise) with the parabola. Together they form a quartic curve, the closed part of which is now on the inside.

Most considerations are internal, but their manifestation will be presented beautifully.

Well-posed

Initial value problems (IVPs) for equations on graphs come in four flavours: under-determined, over-determined, nearly well-posed, and well-posed. An IVP is well-posed if for generic initial values a solution exists and is unique. In Well-posed, one can specify values to the black dots (aka the Cauchy subgraph) and use an integrable equation, on each kite, to determine the value of each white dot. The graph in Well-posed is called the deltoidal trihexagonal tiling.

The Cauchy subgraph in Well-posed is not connected. There is one connected component, comprising seven initial values, and infinitely many isolated components. The connected component plays a special role. It represents the seeds, a small bang. It is where evolution begins.

In Well-posed, all colours mingle, and those of the connected component reappear, scattered.  

The Pappus configuration

Pappus of Alexandria (290-350) was a Greek mathematician, a teacher and prolific writer, who wrote mainly about the works of others but had a sharp eye for mathematical gems which may have been lost otherwise.

The Pappus configuration, of nine points and nine lines, eventually lead to the development of projective geometry.

Take two lines l and l’, such that each line contains three points; l contains a,b,c and l’ contains a’,b’,c’. Consider the three pairs of lines ab’-a’b, bc’-b’c, and ac’-a’c. Their intersection points are on a straight line.

Thus, we have nine lines with three points each, and three lines through each of the nine points.

Hexagrammum mysticum

Blaise Pascal (1623-1662) was a French mathematician, physicist, inventor, philosopher, writer, theologian, and child prodigy. He was only 16 years old when he discovered and wrote about the Hexagrammum Mysticum.

Whenever a hexagram inscribes a conic section the intersection points of the lines through its opposite sides are on a straight line. This line now bears his name: The Pascal line.

Rise and fall of the rainbow

Level sets of an antisymmetric cubic polynomial, cf. Antisymmetry.

A reminder that the world goes ‘round, and opposite forces interrelate. Hope is rising, and tears are in the same basket.